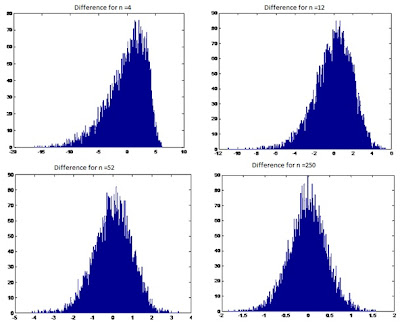
The code below take the time steps as the input and display the difference between the delta hedge portfolio and the actual value for the call option and the standard error. The code also plots the histogram for that particular scenario(Y axis is number of occurrences in total and X axis is difference from the actual value) The histograms below compare the output of histogram for different values of rebalancing time (Denoted as n). The observation from this and the table for differences is that the delta hedge becomes more “efficient” as we increase the number of rebalancing steps. The x axis for n = 4 goes till +/- 20 while for n=250 the max deviation is reduced to +/- 2. Hence we can confidently say that delta hedging become more efficient as we increase the number of steps and it would eventually give zero difference with the actual value when n -> infinity.
Matlab Code:
%The function is checking the effectiveness of delta hedge
%by using Monte-carlo simulation Rebalancing time can be calculated
%Submitted By : Tanmay Dutta
%Simulation method for option Pricing
function [Difference,standard_error]= delta_hedgeH3_1(Rebalancing_time)
% Define the parameters for the option
K = 105;
T = 1;
n = 10000;
N = Rebalancing_time;
S0 = 100;
sigma = 0.1;
r = 0.05;
c = blsprice(S0,K,r,T,sigma,0.0);
% Define what are needed for calculations
Z = randn(n,N);
S = zeros(n,N);
t_increment = T/Rebalancing_time;
timeToMaturity = T-t_increment;
S(:,1)=S0*exp((r-0.5*sigma*sigma)*T/N+sigma*Z(:,1)*sqrt(T/N));
Delta_prev = calculate_callDelta(S(:,1),K,r,sigma,timeToMaturity);
Stock_Position_P = Delta_prev.*S(:,1);
Bond_Position = c-Stock_Position_P;
for i = 2:N
Bond_Position = Bond_Position*exp(r*t_increment); %Bond has grown to this value
S(:,i)=S(:,(i-1)).*exp((r-0.5*sigma*sigma)*T/N+sigma*Z(:,i)*sqrt(T/N)); % New stock process
timeToMaturity = timeToMaturity-t_increment; % time has passed
if i
Stock_adjustment = (Delta_new-Delta_prev).*S(:,i);
Bond_Position = Bond_Position - Stock_adjustment;
Stock_Position_P = Delta_new.*S(:,i);
else
Stock_Position_P=Delta_new.*S(:,N);
end
Delta_prev = Delta_new;
end
Final_value = Stock_Position_P+Bond_Position;
%hist(Final_value,500);
call = max(S(:,N)-K,0);
%figure;hist(call,500);
Difference = Final_value-call; %-max(S(:,N)-K,0);
hist(Difference,500);
title(strcat('Difference for n =',num2str(Rebalancing_time)));
standard_error=std(Difference)/sqrt(n);
Difference = mean(Difference);
end
function delta = calculate_callDelta(S0,K,R,Sigma,T)
delta = (log(S0/K)+(R+0.5*Sigma^2)*T)/(Sigma*sqrt(T));
delta = normcdf(delta);
end