%This code is written by Tanmay Dutta
function val=ABM_simulation(time,step)
delta=(time/step)^0.5; %This is how we define the delta in BM
p = 0.5; % probability of random walk up or down
val=zeros(1,step);
u=zeros(1,step);
for i=1:numel(u)
u(i)=rand;
%%%%% NOTE ' ' NEAR GREATER AND LESS SIGNS. IF
%% YOU WANT TO REUSE THE CODE REMOVE ' ' IN NEXT LINE
val=delta*(p'<'u)-delta*(p'>'u);
end
for k=2:numel(val)
val(k)=val(k)+val(k-1);
end
val(1)=0.00 % Because B(0) =0 always
end
One simulation result for my code :
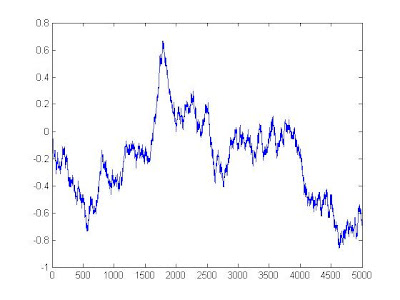
(Simulation on T=[0-1] and step = 5000)
(Note that the level goes below zero too, hence it can not be used for stock modeling and we need geometric Brownian motion with drift for that case )